[最も選択された] ベクトル合成画像 978708

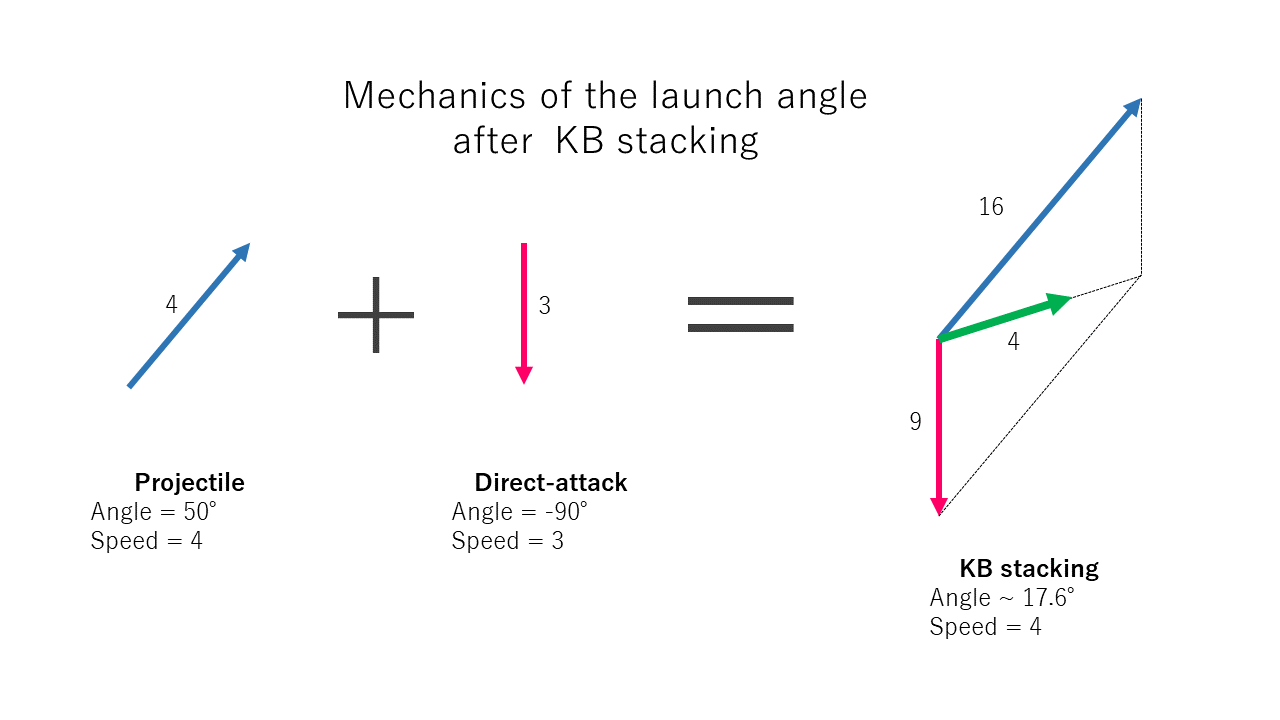
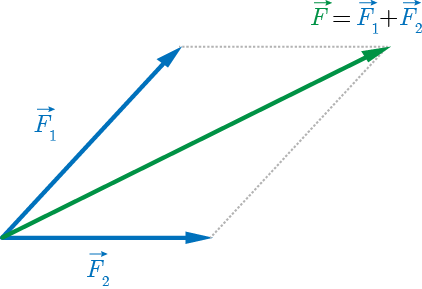
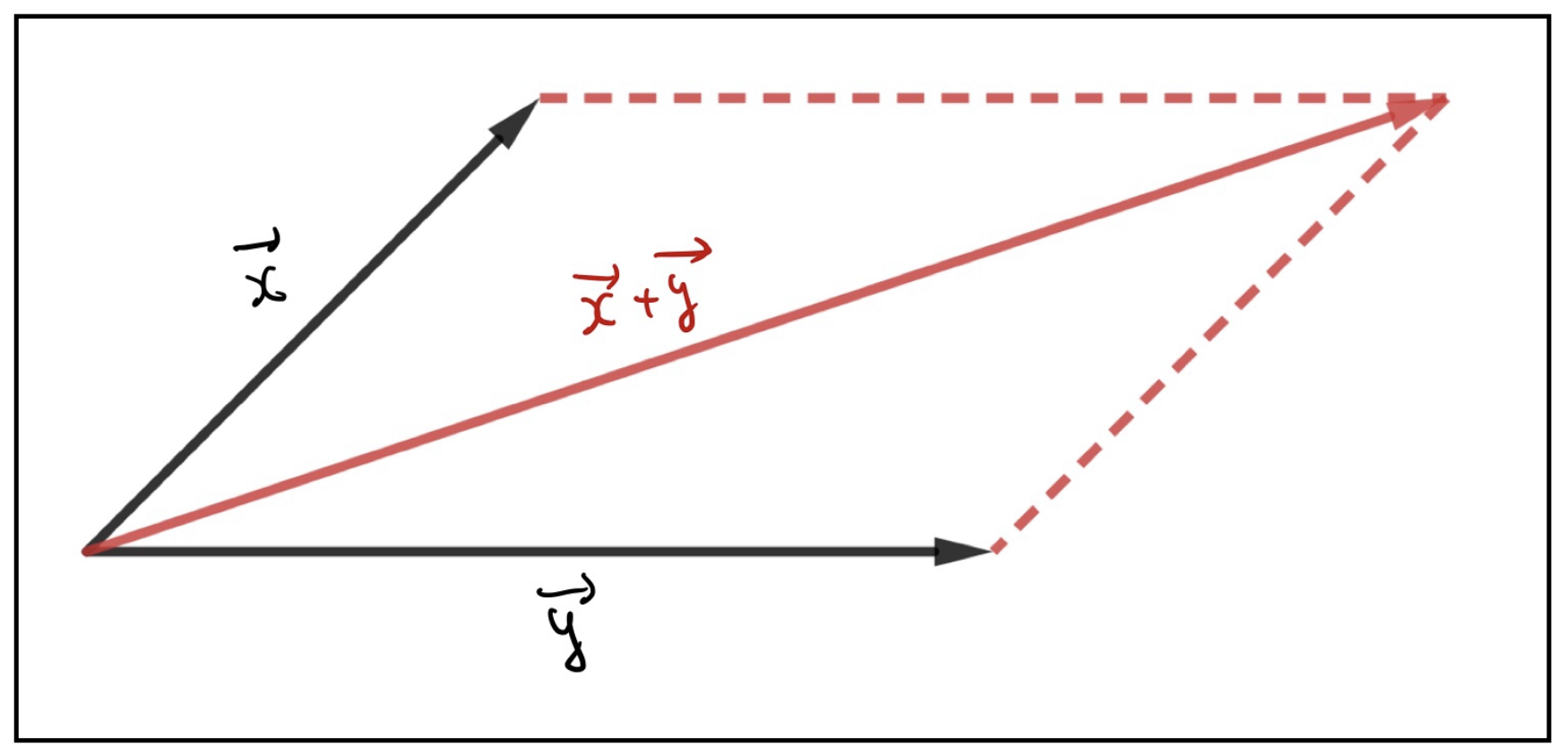
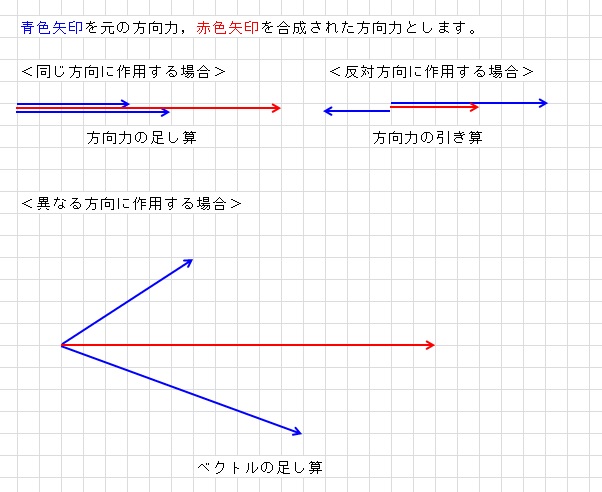
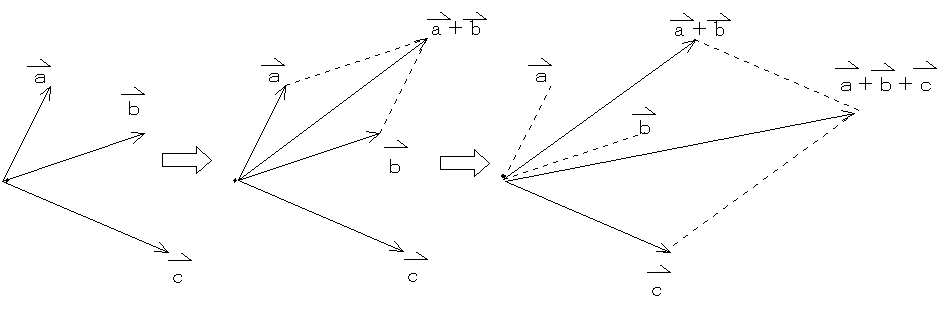
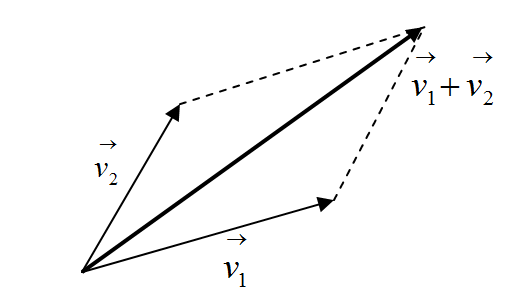
2つの風が重なり合う、2つの力が合成されるなど、2つのベクトルを加えるという感覚は、直感的にわかりやすいものです。 まず幾何学的表現のベクトルについて、次のような2つのベクトルの和を考えましょう。 （右図の右は、その説明画像）集合 a の各要素を集合 b の要素に対応させる規則を a から b への写像という． 写像のうち特に元の集合と対応させる集合とが同一であるものを変換という．（ある集合 a から集合 a 自身への写像） ここでは，さらに限定して変換のうちで対応の規則が「定数項のない1次式」で表される1次変換たとえば、マルチスペクトル画像は 3 バンドのカラー合成 (rgb カラー合成) を使用して表示でき、ここでバンドを使用して関心のあるフィーチャをハイライト表示できます。 配色に沿って値を表示することで、他のエリアより明るいエリアを示すこともでき

ベクトル合成 スマブラfor 3ds Wiiu 検証wiki Atwiki アットウィキ

ベクトル合成画像

ベクトル合成画像- Photoshop（チュートリアル一覧） Photoshopガラスボトルを透過させ光や影をつけリアルな合成を作成 ガラスボトルを背景に透過させ光や影を作成し合成してみました。 使用した画像 ・ ボトル ・背景画像 ＊ボトルの画像は使用長方形選択ツールで ベクトル値関数と多変数関数の合成関数の微分 ベクトル値関数\(f\mathbb{R} \supset X\rightarrow \mathbb{R} ^{n}\)の値域と多変数関数\(g\mathbb{R} ^{n}\subset Y\rightarrow \mathbb{R} \)の定義域の間に、\begin{equation*}f\left( X\right) \subset Y \end{equation*}という関係が成り立つ場合には、それぞれの\(x\in X\)に対して、\begin

ベクトルの合成と分解 数学b フリー教材開発コミュニティ Ftext

そして、上記の計算で得られた2次元ベクトルの大きさとzを使って最終的なベクトルの大きさを求めます。 3次元ベクトル (x,y,z)の大きさ = √ 2次元ベクトル (x,y)の大きさの二乗 z² = √ x² y² z² 例 3次元ベクトル (1,80,30)の大きさ (長さ)を求める対応画像フォーマット avi、wmv、jpeg、bmp、tiff、png連番 データフォーマット プロジェクト形式、csv形式 ベクトル項目 xy合成、x 、y、相関係数、平均 解析項目 流線、流脈線、流跡線、乱流エネルギー、速度標準偏差、レイノルズ応力、速度勾配テンソルベクトルの長所の一つに次元の数が変わってもその成分が増えるだけで演算法則が変わらない ことが挙げられる 今度はベクトル a を配置する空間として3次元空間を想定する 3次元空間では互いに垂直な3つの軸 x 軸, y 軸, z 軸を用意し, その交点を原点 O と

 合成関数の勾配ベクトル アップロード可能な画像フォーマットは jpg, gif, png の 3 種類、ファイルサイズの上限は 5 MB です。 複数の画像をつなぎ合わせて1つの画像とすることを、イメージモザイキングと呼ぶ。 概略の処理手順は、以下のようになる。 1 特徴点と検出のマッチング 2 幾何学的変換の推定 3 画像の幾何学的変換と合成 特徴点の検出とマッチングC = horzcat(A1,,,An) は A1, , , An を水平方向に連結します。horzcat は水平に連結する配列に対して大かっこを使用することと同じです。 たとえば、A と B が互換性のある配列の場合、A,B または A B は horzcat(A,B) と等しくなります。

行列の拡張 1 つ以上の要素を行列に追加するには、既存の行と列のインデックス境界の外に配置して実行できます。 MATLAB は、行列を四角形に保つために、自動的にゼロをパディングします。 たとえば、2 行 3 列の行列を作成して、要素を (3,4) の位置に波のベクトル表記：波の振動方向を決める 緑矢印 振動方向：x軸 青矢印 振動方向： y軸 45゜の場合：波のベクトル表記が便利 波のベクトル表記が便利 一般化：各振動成分が非零の場合 φ ：初期位相 ψ ωφ ψ xx(r, cost t)= −A x ( kr ) ψ(r, ,0,0t)=( ) ψ ωφ ψベクトルとは何か。 その意味とベクトルの足し算・引き算 財布の中に 0 円ある。 いま、その財布の中に 300 円を入れた。 このとき、財布の中には 何円 入っていますか？ 答えは、 0 300 = 500 円ですね。 このように、多くの算数・数学の問題では

ベクトル 高校物理の備忘録

力の合成 分解

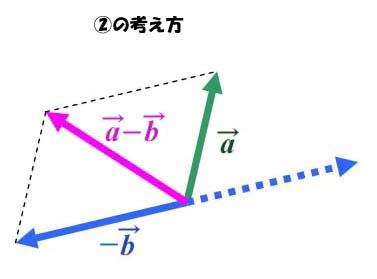
ベクトルの引き算の求め方と計算方法の初心者のための解説 ベクトルの引き算は、幾何学的には、反転したベクトルとの和で求めることができます。 成分表示においては、単純にそれぞれの座標ごとに引き算をすることで求めることができます。 b bベクトルの合成と交流電気回路計算 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会 正弦波交流回路の電圧、電流は、本来、瞬時値計算しなければならないが、定常状態に限って言えば、系統各部の電圧、電流の大きさの比、位相差は一定勾配ベクトルの表記： ©wikipedia ©wwwmathworkscojp Shin Yoshizawa shin@rikenjp 1階微分は接線、傾き Shin Yoshizawa shin@rikenjp 重要：画像のエッジ 画像の勾配画像を高さ関数と考えたときの勾配ベクトル 場、画像のエッジ部分で大きい勾配ベクトルをもつ画像

ベクトルの合成 ぽこラボ勉強ブログ

合成磁場ベクトルの足し算でi 2 2pa I 2 2pa I 2paが Yahoo 知恵袋

 ベクトルでの式と似ていますが、ベクトルで書くと1つにまとめられるのでスッキリしますね。 実は、ベクトルの分野でも、標準三角形とベクトルの演算で、重心のベクトルについて考えています。このときは\ \overrightarrow{ \mathrm{ AG } }=\frac{\overrightarrow 1 1 回答 電界の合成について質問です。 この画像の問題で点電荷A,Bによる点Cでのそれぞれの電界を出すまではいいんですが、電界の合成はそれぞれの電界の和ということで画像のように共にk＊Q/ (√2＊a)^2なので 電界の合成について質問です。 この画像 Excel（エクセル） 縦軸のみのベクトル合成 計算 エクセル 関数 縦軸ののみのベクトル合成の計算を関数で行いたいです。 例えば、A点 1433、B点 7、C点 1002 質

三相交流ベクトル合成について 対称三相交流の相電圧eabcが合 Yahoo 知恵袋

数b ベクトル この問題がわかりません ベクトルa ベクトルb とか ふ 数学 教えて Goo

 簡単にいうならばこんな感じ。 外積とは 2つのベクトル a と b は、0より大きな長さをもち、かつ、同じ向きでも逆向きでもありません（つまりなす角が0度でも180度でもない）。 その時、これらの外積を「 a × b 」という風に記します。 外積は、内積と そこで、「互いに直角を向いていて」「長さが同じ」のベクトルを3本選ぶことにしましょう。 長さが1で、互いに垂直な3ベクトルで構成された座標系 { O a →, b →, c → } のことを 直交座標系 と呼びます。 空間座標の世界では、分かりやすさや使いやすさ合成処理部は、動き情報に基づきグローバル動きベクトル、ローカル動きベクトルを算出し、動きベクトルに基づき画像を合成する。 例文帳に追加 The composition processing part calculates a global motion vector and a local motion vector based on the movement information and composites the

この問題がよくわからないです 教えていただける方よろしくお願いします Clearnote

ベクトル合成 スマブラfor 3ds Wiiu 検証wiki Atwiki アットウィキ

2つのベクトルの角度を求める方法 数学において、ベクトルは定義可能な長さ（大きさ）と向きを持つ量のことです。普通の線や図形とは異なり、ベクトル間の角度を求めるには特別な公式が必要です。 コサインについての公式を書く 2つのベクトルの角度θを知るために、角度のコサインを撮影・画像合成 まるで生きている。 写真は人が目で見ている映像の中で一番良い部分を1コマだけ切り取って見せる事。 何も言葉をそえなくても、それで全てを物語れる力を持っている。 人物は活きいきと、商品は魅力的に、撮影の方法一つで大きく合成変換・逆変換・回転を表す線形変換 逆変換 逆変換 ♣ 線形変換f がすべてのベクトルp を自分自身に写すとき， つまり，f(p) = p であるとき，f を恒等変換という。 恒等変換を表す行列は単位行列E である。 ♣ 線形変換f に対して，合成変換g f が恒等変換になるg を

対称座標法における正相成分と逆相成分 電気の神髄

ベクトルの合成と分解 卓球の物理学 Pp Physics Com

 Excel で角度データの平均を計算するとき、そのまま Average 関数を使って求めているケースを何度も見たことがあります。単純に平均すると問題が起きる場合があることが意外と知られていないようなので、今回は角度の平均について説明してみます。15° と 345° の平均は何度で内積公式や証明・計算問題 21年2月19日 この記事では、ベクトルの「平行条件」や「垂直条件」について、できるだけわかりやすく解説していきます。 計算問題だけでなく証明問題の解き方も解説していきますので、この記事を通してぜひマスターして ベクトル解析の用語は、時空間上の状態変化を記述する偏微分方程式（partial differential equation）の基礎です。また、ベクトル場によって定まる微分方程式系の、解の挙動を調べる理論は、力学系理論（dynamical systems theory）として知られるものです。

16 号 ベクトル合成型移相器およびベクトル合成型移相器の制御方法 Astamuse

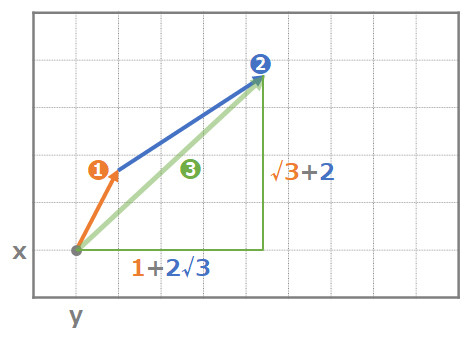
統計学や機械学習でもよく使われる相関係数が分かるベクトル計算の基礎知識 Ai エンジニアになるための 基礎数学 再入門 12 It

 このため、本ブログでは表記を使い分けつつ、必要に応じてベクトルを行列とみなして演算する、といった方法で解説しています。 ベクトルの回転方法 主に、3次元のベクトルを回転させる方法は、大雑把に言って次の3つがあります。1 回転行列 2

３つのステップで物理に登場するベクトルを完璧に使いこなす うさはち物理教室

看板屋 Com

高校物理 便利なベクトルで 変位 速度 加速度 力学 お茶処やまと屋

干渉

ベクトルの表記法とベクトルの合成 やさしい電気回路

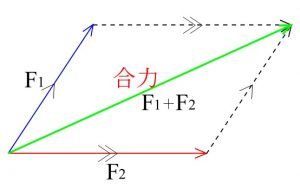
力の合成と分解とは 成分の作図は平行四辺形が基本

1

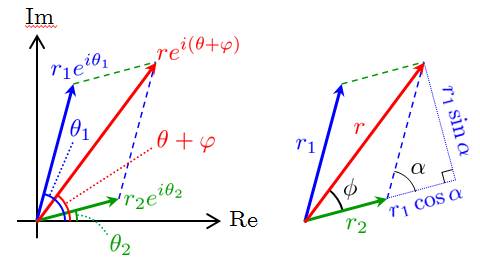
Cos関数の合成 導出

ベクトルとしての力の合成 分解 高校生から味わう理論物理入門

ベクトル図の書き方 基礎の基礎から三相交流まで図解で解説 電験３種一発合格講座

力の作図方法 力の合成と力の分解について 建築学科のための材料力学

樋口の物理教室 力学 4 相対速度 合成速度

高校の問題です 三つのベクトルの合力の求め方が良くわかりません この写 Yahoo 知恵袋

３力のつりあい

ベクトル と 合成速度 について理系ライターが丁寧に解説 ページ 2 2 Study Z ドラゴン桜と学ぶwebマガジン

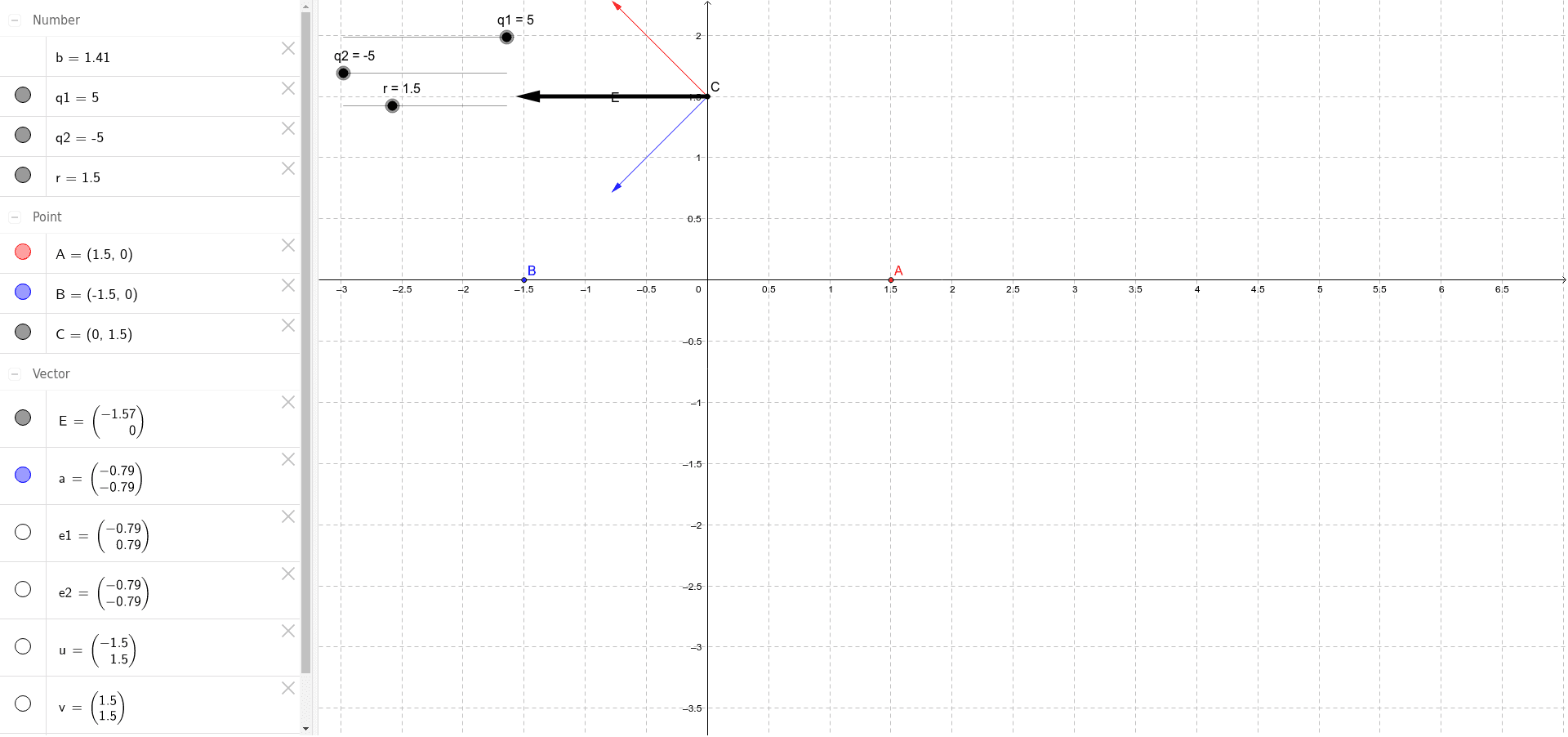
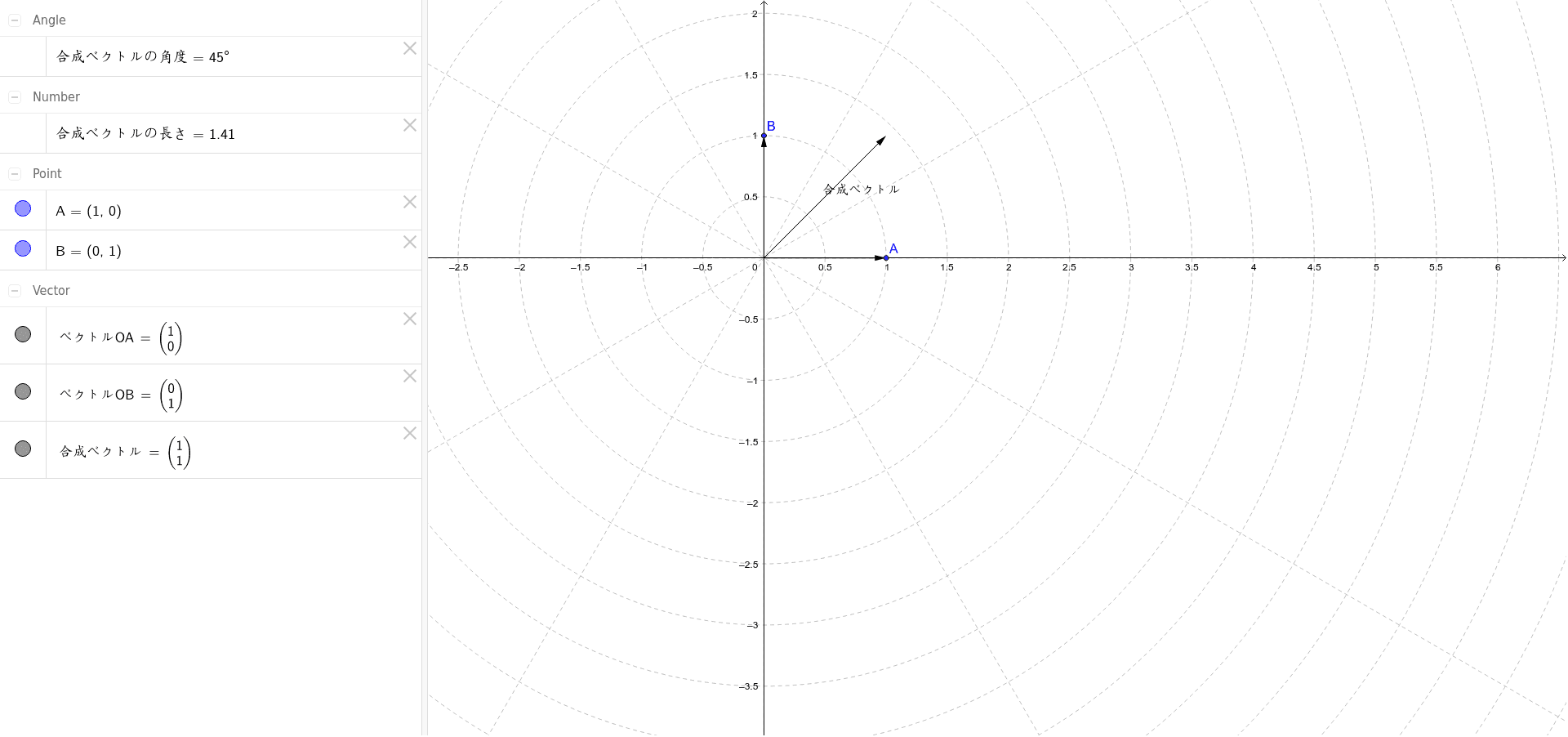
電界ベクトルの合成 Geogebra

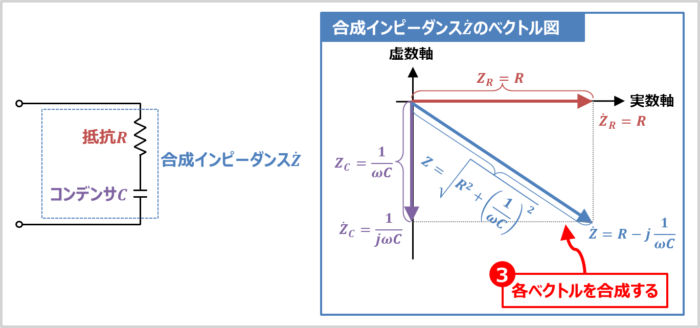
Rc直列回路の 合成インピーダンス を分かりやすく解説

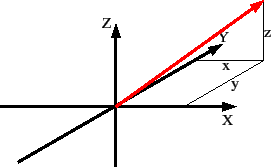
3次元ベクトル

ベクトル プロット Vector Plots 12 Solidworks ヘルプ

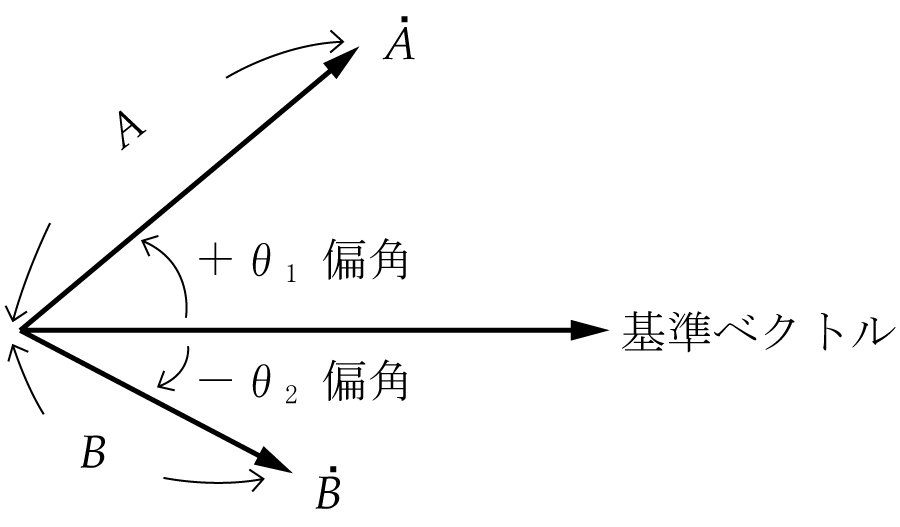
ベクトルの合成と交流電気回路計算 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会

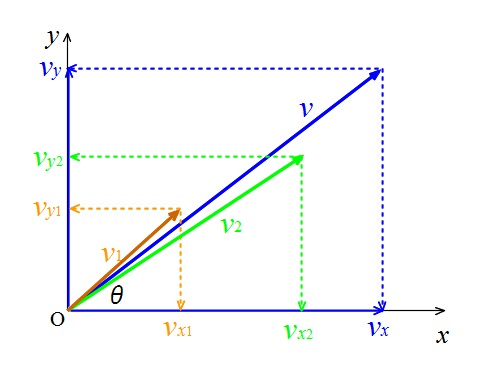
速度の分解と成分の表し方と合成

物理点電荷のベクトル計算について このベクトルeaとeb Yahoo 知恵袋

ベクトル 高校物理の備忘録

ベクトル 行列を含む微分 Taustation

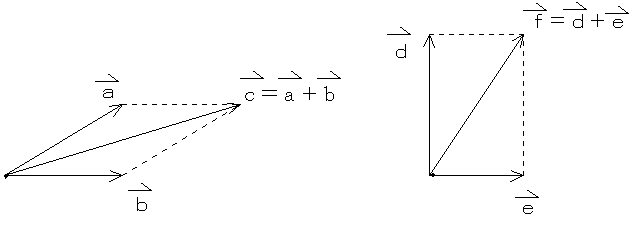
力の平行四辺形

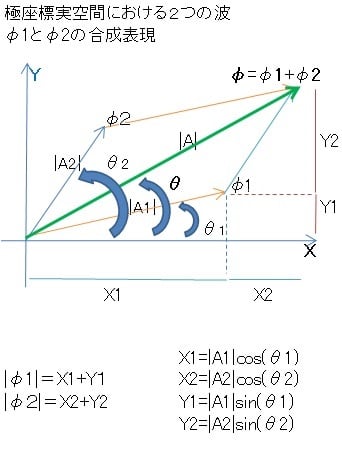
合成された波の強さ まとめ 複素平面座標と直行座標の比較 空観方程式

ベクトルの合成と分解 数学b フリー教材開発コミュニティ Ftext

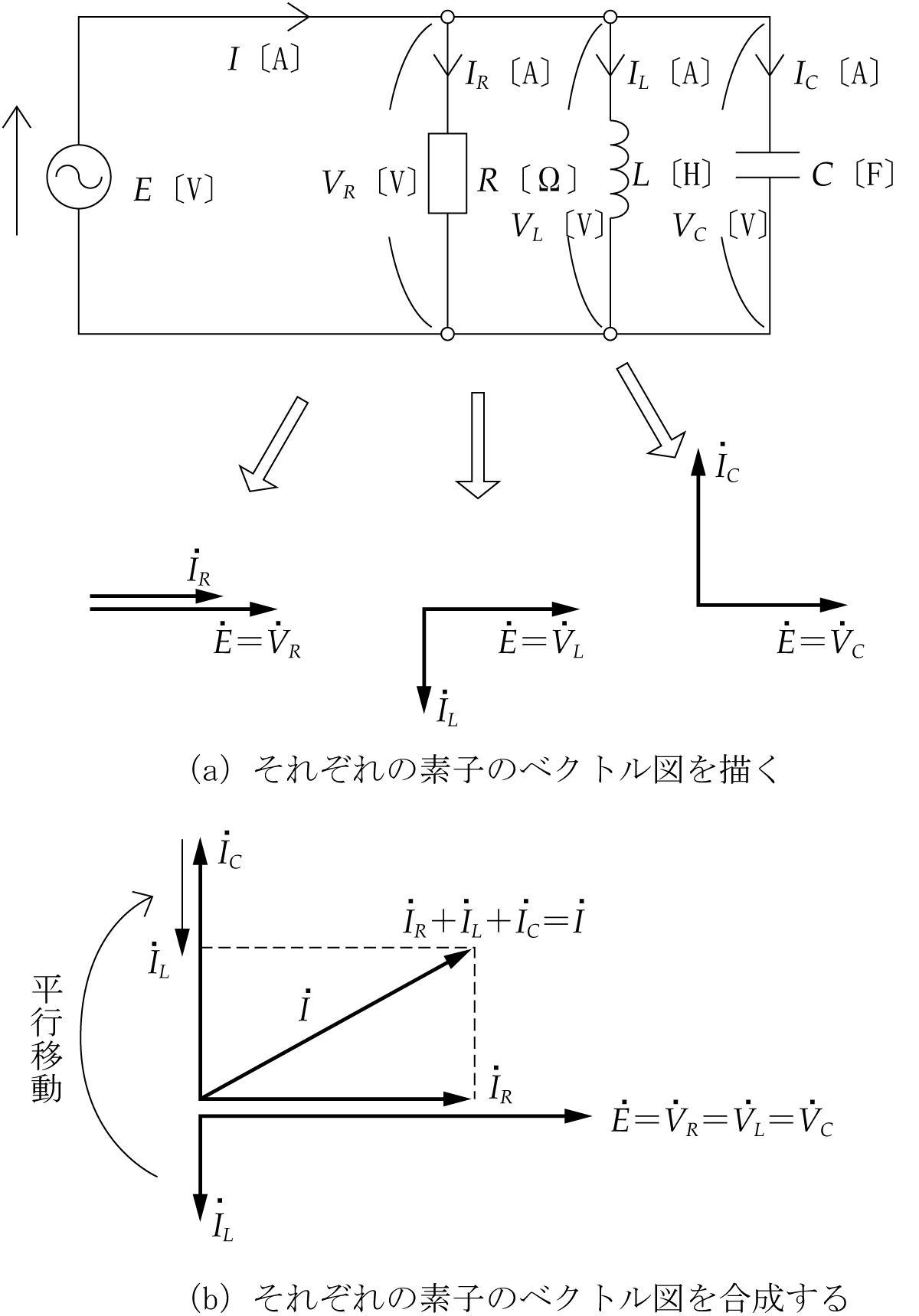
ベクトルの合成と交流電気回路計算 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会

中古 ケイビーエフ Kbf アーバンリサーチ スクエアトゥブーツ ショート ミドルヒール 合成皮革 シューズ ベクトル 黒 13 レディース 特価品コーナー 36 ブラック レ 古着

力の作図方法 力の合成と力の分解について 建築学科のための材料力学

力の作図方法 力の合成と力の分解について 建築学科のための材料力学

力の合成と分解 初心者のための力学入門 Pei S Lab

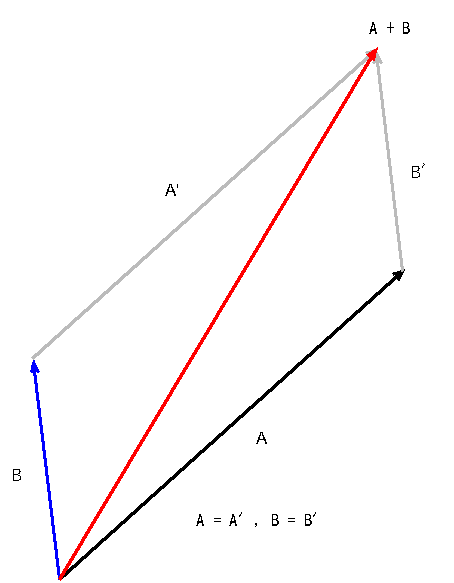
潮流航法はベクトルの合成

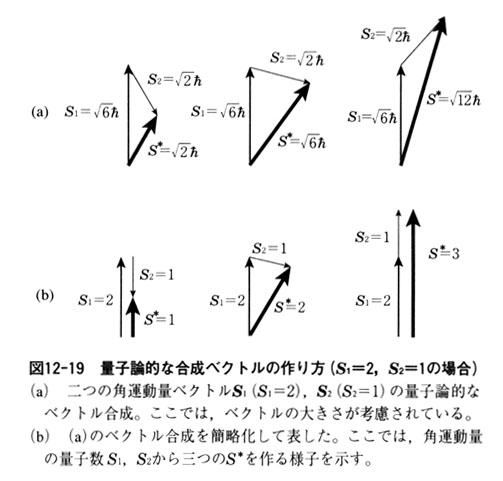
図12 19 量子論的な合成ベクトルの作り方

ベクトル ベクトルの基礎概念

勉強しよう数学 空間ベクトルの３つの公式

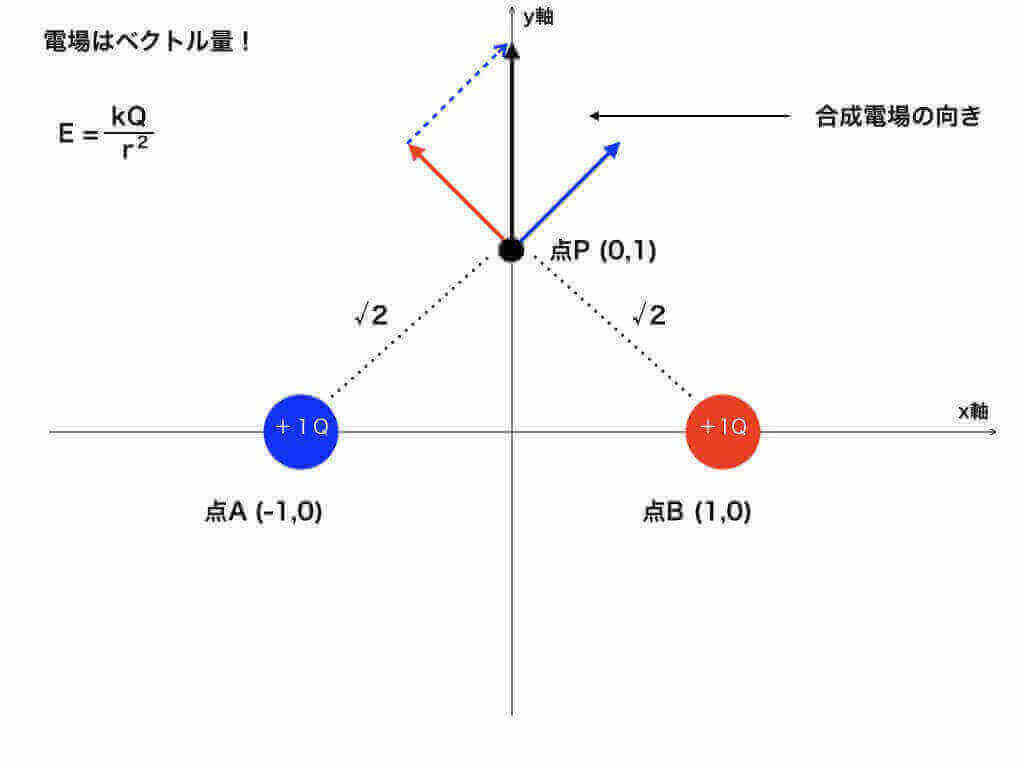
複数の点電荷による座標上の電位の計算と力学との融合問題

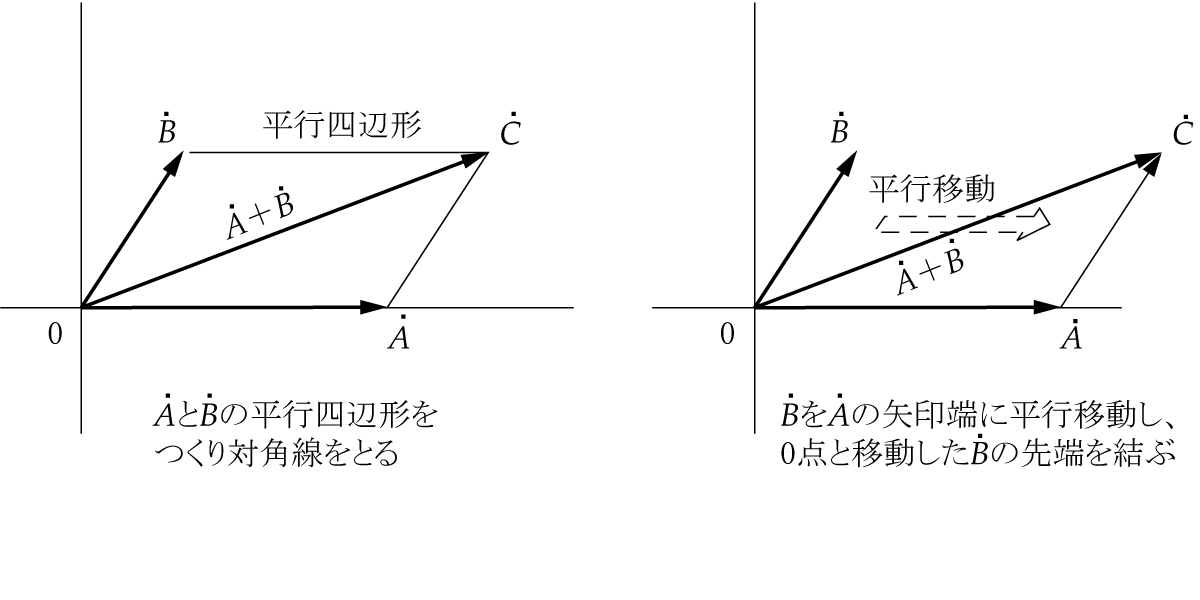
ベクトルの合成と交流電気回路計算 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会

物理基礎 速度の合成と分解 公式を使って実際に問題を解いてみる Himokuri

3

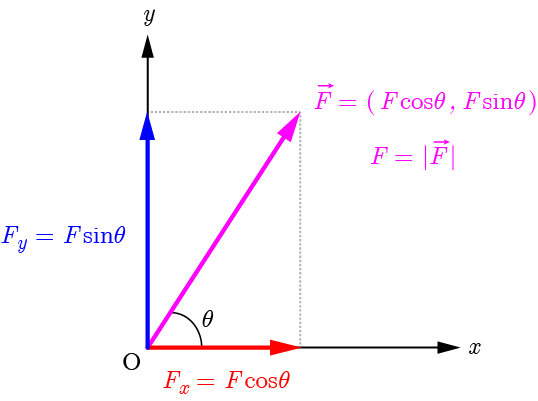
力の合成 分解

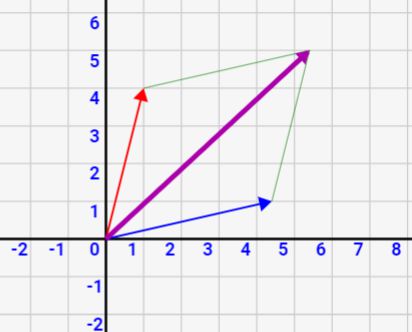
物理入門 合力 力の合成 2次元 3次元 をシミュレーターを用いて理解しよう

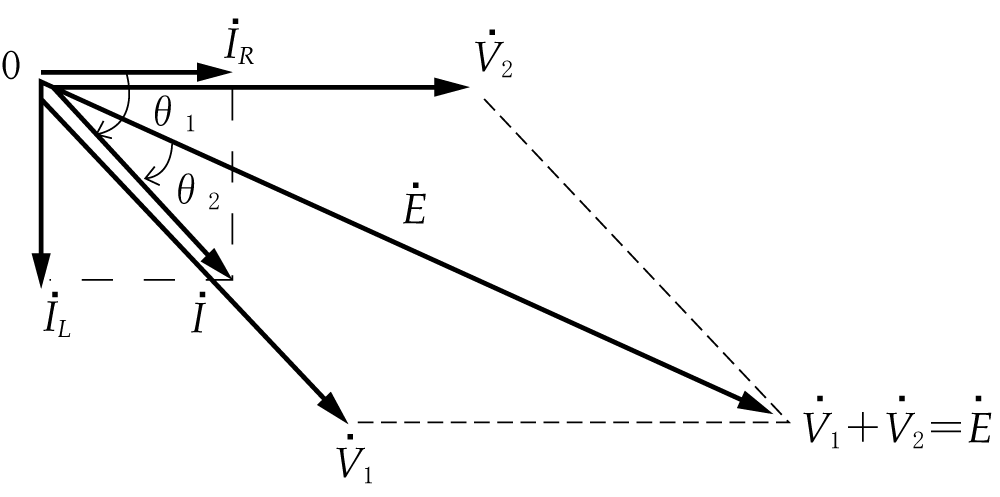
ベクトルの合成と交流電気回路計算 音声付き電気技術解説講座 公益社団法人 日本電気技術者協会

高校物理 合成電場 映像授業のtry It トライイット

ベクトルとは 足し算引き算 合成 や成分表示について分かりやすく簡単に解説 遊ぶ数学

ベクトル 高校物理の備忘録

図解 力の性質とベクトルについて理解を深めたい人へ 物理基礎

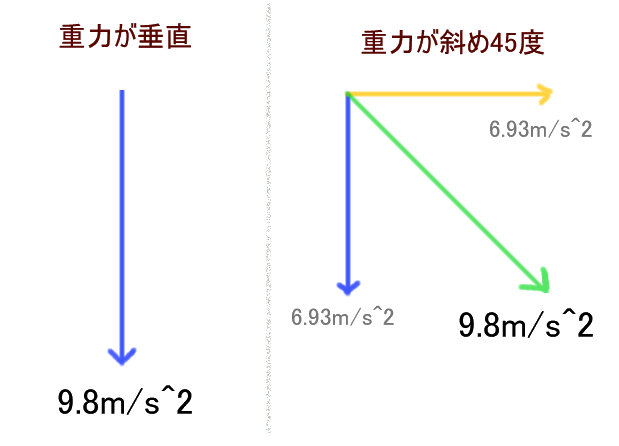
グレイ Pa Twitter そういえば 重力加速度の値をそのままにして重力方向にy以外の要素を入れると 垂直方向の加速度は減少するのだよな つまり重力方向を弄って風や横gを表現したい場合 重力加速度 は合成ベクトルの大きさだから 9 8のままでは垂直成分 本来の重力

ベクトル と 合成速度 について理系ライターが丁寧に解説 Study Z ドラゴン桜と学ぶwebマガジン

ベクトルを使って三角関数を合成 Youtube

力の合成のまとめ 建築士の必要知識

力の平行四辺形

超必須事項 ベクトルの合成 と分解 文系にこそ読んでほしい高校物理のコツ文系にこそ読んでほしい高校物理のコツ

交流回路ベクトル図の書き方 基礎から直列回路や並列回路まで 電験３種一発合格講座

1

速度はベクトル 速度の合成 分解 タイトル 仮 大学講師が解説 高等学校学習指導要領から学ぶ物理学

ベクトル合成

佐賀 Net

ベクトル と 合成速度 について理系ライターが丁寧に解説 Study Z ドラゴン桜と学ぶwebマガジン

ベクトルとしての力の合成 分解 高校生から味わう理論物理入門

合成ベクトルを図示せよという問題なのですがわかりません お願いします Yahoo 知恵袋

勉強しよう数学 三角関数の合成の公式

ベクトルの和

勉強しよう数学 3次元ベクトルの分解の公式

ベクトル２

物理ネコ教室005ベクトルの合成と分解 ひろじの物理ブログ ミオくんとなんでも科学探究隊

ベクトルの合成と分解 数学b フリー教材開発コミュニティ Ftext

ベクトルの合成 Geogebra

ベクトル と 合成速度 について理系ライターが丁寧に解説 ページ 2 2 Study Z ドラゴン桜と学ぶwebマガジン

16 号 ベクトル合成型移相器およびベクトル合成型移相器の制御方法 Astamuse

覚えなくていい 三角関数の合成 東大生の高校数学ブログ

物理の授業 ベクトルの合成 あなたと夜と数学と

Hasegawa Susumu ベクトルoa ベクトルob ベクトルoc のy成分を比較すれば Sin の合成公式が得られる 理系上位生向けの春期講習会の この時期こそ まずは基本事項を確認しよう というテキストの基本事項に載せたもの T Co Edr99qkcuh

06 号 音声合成装置および音声合成プログラム Astamuse

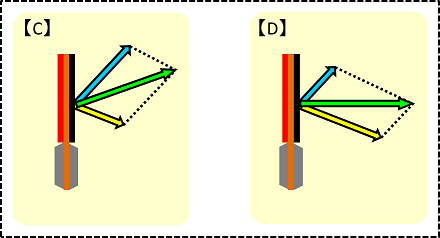
Komaさんの卓球 7 2 スピン合成とベクトル表記の考察

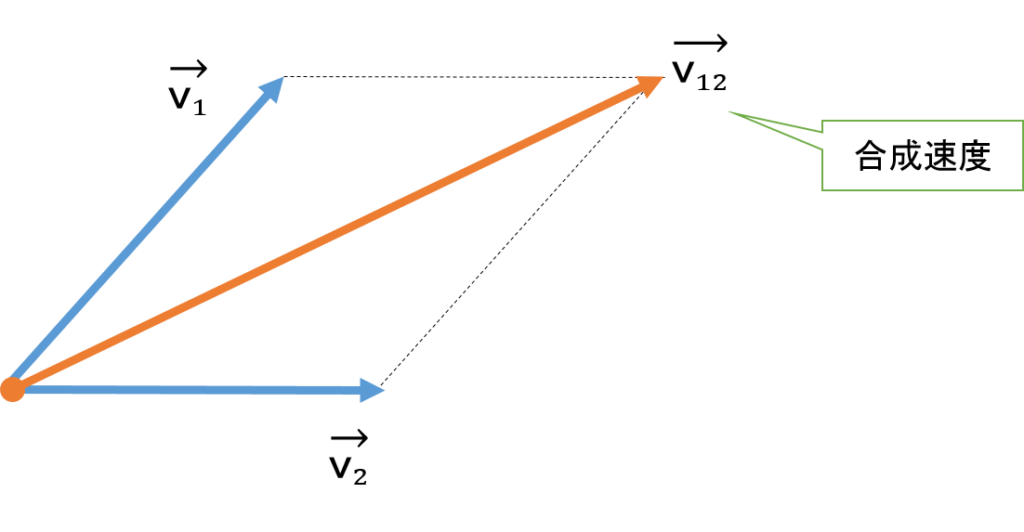
合成速度 相対速度 矢印 ベクトル での描き方の違いを説明 平川ブログ

力の作図方法 力の合成と力の分解について 建築学科のための材料力学

わこー Rwumxqhclek4nes Twitter

同期機のベクトル図導入

ベクトル と 合成速度 について理系ライターが丁寧に解説 Study Z ドラゴン桜と学ぶwebマガジン

ベクトルとは

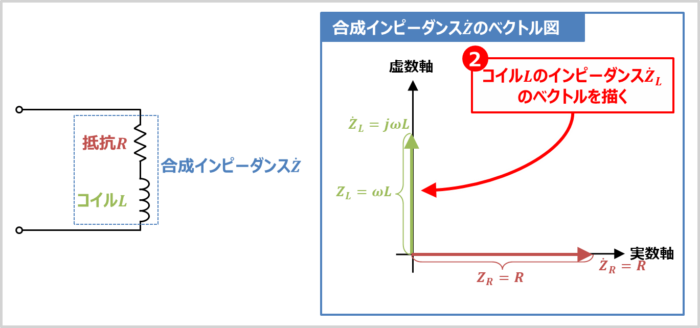
Rl直列回路の 合成インピーダンス を分かりやすく解説

電験どうでしょう 新電気でコラム連載中 En Twitter 朝活どうでしょう 解答編 正三角形の重心の特徴をうまく使ってベクトルの合成 をしてみましょう 点pでは同じ大きさの3つのベクトルが1 ずつずれて存在することになります 成分に分けて合成すると結果は0

次のベクトルf1とf2の合成ベクトルを図示し X Y成分と大きさを求めたいので Yahoo 知恵袋

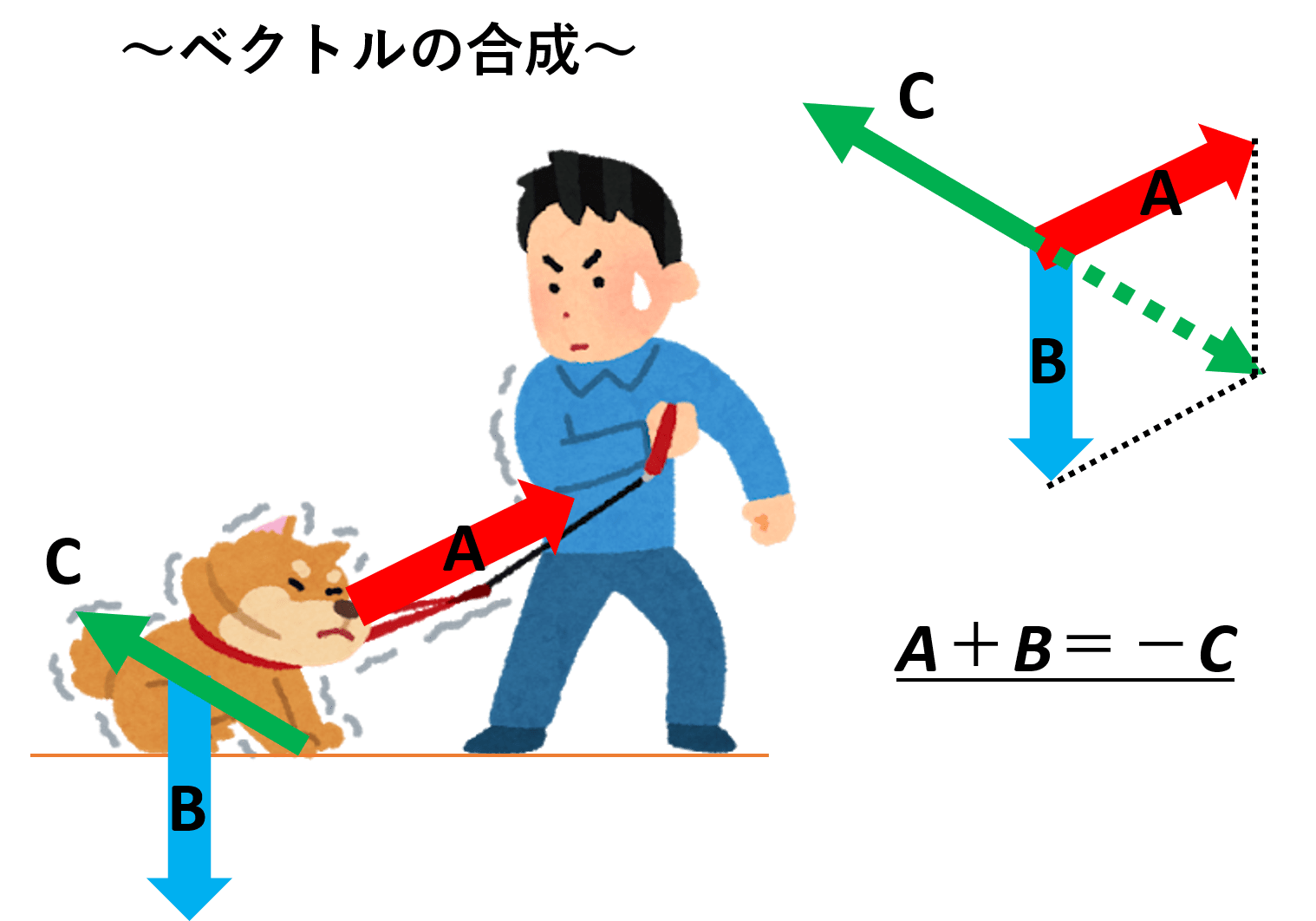
力 速度の合成と分解 ベクトル合成と分解 陸上競技の理論と実践 Sprint Conditioning

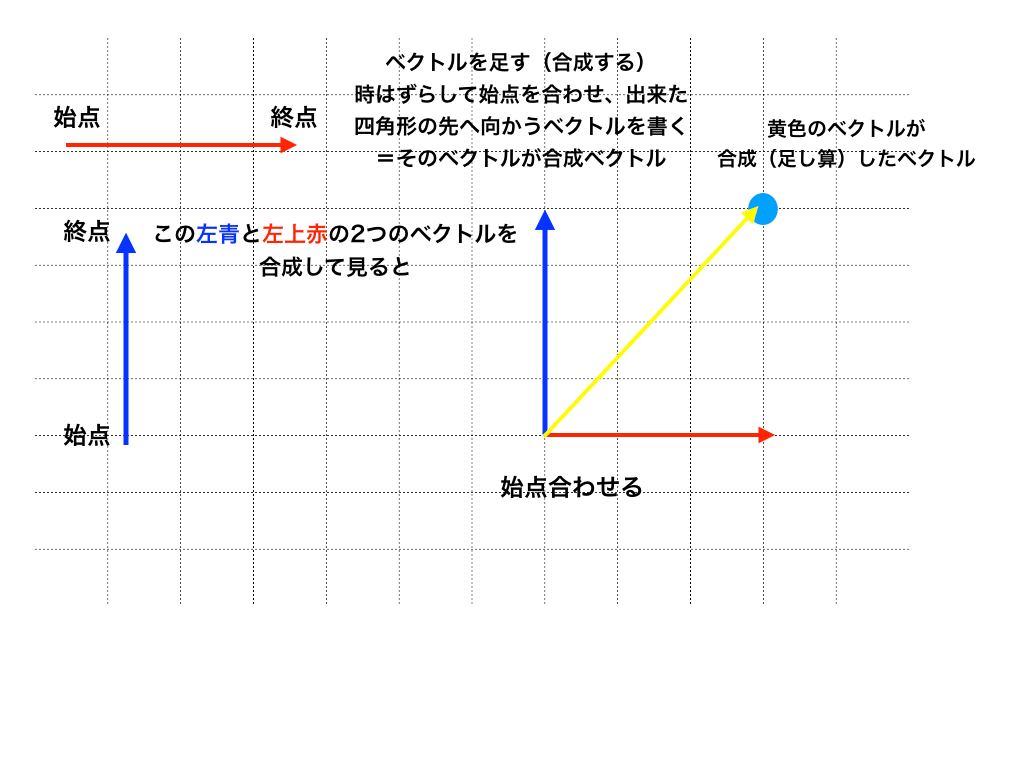
物理基礎で使うベクトルを0から解説 力学で困らない為の数学

速度の合成と分解 高校物理をやさしく解説するブログ

1

なぜ 点電荷a Bがそれぞれｐにつくる電場eaベクトル Ebベクトルは 向き Clearnote

高校物理 合成電場 合成電位 練習編 映像授業のtry It トライイット

ベクトルの合成分解の計算方法 3d Cad Cae 解析と物理の学習まで無料版simulationxpress 使い方入門編

物理の力の合成の問題です １ 力ベクトルf1とベクトルf2の合力 Yahoo 知恵袋